E = electromotive force (EMF) in Volts (V), also called Potential Difference (PD), or Voltage.
V is a less used alternative symbol for EMF in the SI or MKS system.
I = current in Amperes (A),
R = resistance in Ohms (Ω),
G = conductance in Siemens (S),
P = power in Watts (W).
C = capacitance in Farads (F),
L = inductance in Henrys (H).
X = reactance in Ohms (Ω),
B = susceptance in Siemens (S),
Z = impedance in Ohms (Ω),
Y = admittance in Siemens (S),
f = frequency in cycles per second (c/s), or Hertz (Hz)
Q (Quality), has no units, it is circuit magnification, the ratio of reactance to resistance. With a tuned circuit, refers to selectivity.

Ohm's Law: Current = EMF (Voltage) divided by resistance.
The three forms of the equation are: I = E/R, R = E/I or E = I X R

Power: Watts = Voltage multiplied by current.
W = E X I = E²/R = I² X I

One Horsepower (HP) = 746 Watts to the nearest integer, in Britain & America. To be be more exact it is 745.699872 Watts, the origin is 33,000 foot-pounds per minute or 550 foot-pounds per second. This was calculated by James Watt after measuring the work that pit ponies could do.

At one time the term 'brake horse power' or B.H.P. was used. This was because the standard measurement method involved absorbing the power in a weighted belt on drum brake. A means was needed to distinguish it from the archaic RAC automobile horsepower rating, which was essentially meaningless for modern engines.

A human athlete can produce about half a horsepower for extended periods. Some can achieve around 1.25 to 1.75 horsepower for brief sprints.

They specify 750 Watts in Europe, a big place, they need slightly bigger horses.

Resistors in parallel: Easiest to work out using conductance. Total conductance G is the sum of the individual conductances.
G = 1/R1 + 1/R2 + 1/R3 etc. Then: R = 1/G
Another way sometimes quoted for 2 resistors is the product divided by the sum, (R1 X R2)/(R1 + R2). I personally cannot see the point in this 'short cut', it is more difficult.

Capacitors in series: Total capacitance C is the reciprocal of the sum of the individual reciprocals.
1/C = 1/C1 + 1/C2 + 1/C3 etc. Alternatively: C = 1/(1/C1 + 1/C2 + 1/C3 etc.)
Another way for 2 capacitors is the product divided by the sum, (C1 X C2)/(C1 + C2)

Inductors in parallel: Total inductance L is the reciprocal of the sum of the individual reciprocals.
1/L = 1/L1 + 1/L2 + 1/L3 etc. Alternatively: L = 1/(1/L1 + 1/L2 + 1/L3 etc.)
Another way for 2 inductors is the product divided by the sum, (L1 X L2)/(L1 + L2)

These equations work equally for multiples or sub-multiples of the base unit. Microfarads, millihenrys, Kilohms etc. Provided the same multiple etc. is used for each component.

Rather as a spring is compressed by a weight, returning stored energy by helping lift the weight.

Measured in Ohms (Ω). Series or parallel reactances, of one type, can be calculated using the same formulae as resistances.

Capacitive reactance: X_C = 1/2πfC

Inductive reactance:     X_L = 2πfL.     π (pi) = 3.14159 to 5 decimal places.

Susceptance, B, is the degree of ability of a simple reactance to conduct current. It is thus the reciprocal of reactance & is measured in Siemens (S).

Impedance Z is the complex vector combination of resistance & reactance in a practical circuit. Real circuits always have resistance, capacitance & inductance. Measured in Ohms (Ω).

Admittance, Y, the ability of a complex circuit to conduct current, is the reciprocal of impedance. Useful for calculating parallel impedances, it is measured in Siemens (S).

A coil & capacitor can be wired in parallel. Forming a tuned circuit, with a resonant frequency. At resonance the reactance of both components is equal. According to classical theory, current through a capacitor leads the Voltage by 90 degrees, that through an inductor lags by 90 degrees. Thus the two currents are 180 degrees out of phase.

Since they are equal at resonance, they cancel exactly, no net current flows.

So at resonance the combination exhibits infinite reactance. In parallel with this are circuit losses, essentially resistive, forming a finite impedance, nothing is perfect. In a practical circuit the ratio of frequency at resonance, to bandwidth is termed Q (quality). For RF this is typically around 50 to 100.

At low audio frequencies it is often less, due to practical component size & cost limitations.

Bandwidth is the difference between the frequencies, either side of the resonant peak, that are 3 dB down or half the power.

Another definition of Q for some purposes is circuit magnification. The ratio of impedance or gain at resonance to that at frequencies outside the range of interest. This figure is important in determining the degree of rejection of unwanted frequencies. Thus it may be called 'rejection ratio'. It can be improved, as in analogue radio use, by cascading a number of tuned circuits.

The relevant equations are:

At resonance: X_L = X_C, f = 1/(2π X √(LC)),   Q = f/bandwidth

Resistance (R) is the tendency of materials to oppose the flow of current through them.

Materials that present little opposition are termed conductors. Metals generally fall into this category, as does carbon. Resistors are usually carefully formulated & proportioned conductors.

Materials exhibiting almost complete opposition are called insulators. Most thermoplastics, ceramics, rubber & glass are examples.

Materials with intermediate properties are termed, logically, semiconductors. Examples are germanium, gallium arsenide, and suitably alloyed silicon. These have other properties, making them useful in electronics, particularly when controlled small proportions of suitable impurities are added. This subject requires at least its own page.

Many liquids, particularly aqueous solutions of salts, conduct electricity. The mechanism of conduction is different, so they are also treated separately.

The unit of resistance is the Ohm (Ω), named after Georg Simon Ohm, who formulated his famous law in the early Victorian era. Like many other pioneers he received little recognition in his lifetime. One Ohm allows one Ampere of current to flow when a potential difference of one Volt is applied, ten Ohms will allow one tenth of one Ampere when similiarly provoked.

Conductance (G) is a measure of the ability of materials to conduct current. It is the reciprocal or inverse of resistance. The unit of conductance is the Siemens, symbol S, named after Ernst Werner von Siemens. One Siemens conducts one Amp when one Volt is applied, ten Siemens will similiarly conduct ten Amps. It can therefore be thought of as Amperes per Volt.

A former name for the unit of conductance is the Mho, Ohm spelt backwards. In other respects it is the same

Parallel resistances are most easily calculated by addding their conductances (1/R). The reciprocal of the sum is the total resistance.

A more complete definition of a Volt is: The unit of electrical potential equal to one Joule per Coulomb.

Current (I), is measured in Amperes, named after Andre Marie Ampere. 1 Ampere = one Coulomb (6.24 x 10¹⁸ electrons) per second, passing one point on a conductor. It is also defined as the current through a one Ohm resistor when one Volt is applied.

Electrical current is always a flow of electrons, from negative to positive. In a conductor they do not actually flow directly through, an electron arrives at an atom & joins its outer valency ring. In doing so one already there is displaced. Attracted towards the positive terminal it encounters another atom, displacing a further electron & so on. In a vacuum it is a true electron flow.

In the early days of electrical experimentation it was assumed that current flowed from positive to negative. In other words, that the moving particles were positive charges. This mistake persisted until Dr. A.J. Fleming's invention of the thermionic valve in 1904. His original diode proved beyond doubt that the travelling electrons are negative & flow from negative to positive.

Despite this many physicists, even today, insist that true current flows from positive to negative. Pigheadedly perpetuating a 200 year old mistake, despite a 1 hundred year old proof to the contrary. Books are still published showing 'conventional' current flowing from positive to negative whilst electrons flow the other way.

What a nonsense! When I was at school, in a 'science' class we were shown a so called educational film. This featured, in cartoon form, current flowing one way, whilst electrons went the other. I remember thinking at the time, 'this is rubbish, the opposite charges will collide & cancel out'. This is something they are still trying to push.

Millions of pounds are spent every year on research into positrons (anti-electrons) and anti-protons. Atoms are bombarded in cyclotrons & other mega-expensive machines. Whatever the potential uses for these exotic particles they do not contribute to current flow. They can only be isolated in high energy environments.

A lot of time & money is spent studying the theory of 'anti-matter'. This has atoms with a negative nucleus & orbiting positive charges. It will be handy to provide the astronomical energy requirements for interstellar space travel, along with warp drive & matter transporters.

It certainly can't exist in the same place as normal matter, otherwise the two would cancel. Unleashing a force sufficient to make an atom bomb seem like a firework. So we are not likely to be able to mine it on any planet where we can survive.

Electrical charge is measured in Coulombs, essentially a very small bucketful of electrons, named after Charles Augustin de Coulomb. One Coulomb = 6.24 x 10¹⁸ electrons or 1 Ampere for one second.

Energy, power used or work done is measured in Joules (J). Named after James Prescott Joule, one Joule is 6.24 X 10¹⁸ Electron Volts. Alternative specifications are: 1 Watt-second, 10⁷ ergs, 1 Newton-Metre, 0.2390 calories or approximately 0.738 foot-pounds. The kinetic energy of a 2 kilogram mass moving at 1 metre per second. There are many other equivalents.

Capacitance (C) is measured in Farads, (F) named after Michael Faraday. One Farad is charged to a potential of one Volt by one Coulomb or one Ampere for one second. The Farad is inconveniently large for most purposes. Microfarads (μF), (F X 10^-6), nanofarads (F X 10^-9) or picafarads (F X 10^-12) are in common use.

Inductance (L) is measured in Henrys (H), named after American physicist, Joseph Henry. The induced EMF across a one Henry inductor is one Volt, if the current through it changes by one Ampere per second, 1 H = 1 Vs/A. Convenient sub-multiples are millihenrys (mH) & microhenrys (μH). These are H X 10^-3 & H X 10^-6 respectively.

Frequency (f) is measured in cycles per second (c/s). The European term for this value, Hertz (Hz) is now commonly used. Named after German Phyicist, Heinrich Hertz, the first to publish data on experiments with wireless transmission. Sine waves are cyclic, rotating in phase through 360 degrees continuously, hence cycles per second.

Kilocycles/s, Kc/s (f X 10³), second Megacycles/s, Mc/s (f X 10⁶) & Gigacycles/s, Gc/s (f X 10⁹) are convenient multiples for practical use. Again Hz, instead of the logical c/s, is considered "politically correct" by the 'Establishment'.

There are a number of different methods for measuring AC Voltage & current. The image below represents a sine wave. Clicking on it will link to the Sine Wave page, with more information on derivation etc. The browser's 'Back' button will link back to here.

One cycle of a sine wave, 2π radians or 360 degrees. Plotted against angular displacement.
Moving the mouse cursor to the image will plot the wave. Horizontal scale factor is c/π.
The vertical scale is plus & minus 1 Volt for the purpose of the following discussion.

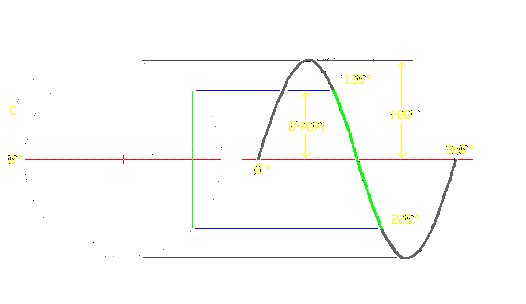
The obvious way is to measure the peak, or the peak to peak value. 1 Volt or 2 Volts respectively for this image. This is a useful means of indicating the electrical 'headroom' required to accomodate the sigmal. It does not however directly give a value for the useful EMF, current or power. The secret here lies in the area enclosed by the curve, bounded by the reference or zero line. This gives the effective or heating power of an electrical waveform. The accepted method of establishing this effective area is called RMS, a standard abbreviation for 'Root Mean Square'. The instantaneous amplitude is measured at a number of equally spaced points along one or more full cycles. Each of these values is squared & the results averaged. The square root of the answer is the RMS value. Some waveforms are fully symmetrical, such as a triangle, square or sine wave. For these only one quadrant needs to be measured to obtain high accuracy. All others need the full cycle, reducing any errors requires more measured points. For a pure sine wave Voltage there is a 'short cut', just one point, at 45 degrees, is precise. Multiplying the peak by the square root of one half (0.7071) gives this figure. Crest factor is the ratio of peak to RMS, 1.4142/1 (√2/1) in this case. This ratio is squared for power into a resistive linear load, it is thus 2/1. Most analogue & digital Voltmeters average the waveform. Scaling is adjusted to the ratio of 1.1118/1 to give an RMS readout, this is generally only accurate for sine waves. Some more expensive meters have the extra circuitry to calculate a 'true RMS' reading. For a triangle wave, the average & RMS readings are the same. With a true square wave, average, RMS & peak are the same. To obtain a true square wave an infinite number of odd harmonics are needed. The transition from positive to negative, or vice versa must occur in zero time. This requires infinite instantaneous power in a real circuit. There is another way to obtain an RMS Voltage reading, regardless of a waveforms harmonic structure. Apply the Voltage across a perfect resistor & measure the temperature rise. This is slow & can suffer from ambient temperature or other losses. A useful technique for difficult waveforms, such as noise & narrow or asymmetric pulses. Ratios denoted by the most common deciBel values.   dB     Voltage       Power         dB     Voltage       Power     0.5 1.06 1.12   25 17.8 316.23 1 1.12 1.26   30 31.623 1000 2 1.26 1.58   35 56.29 3,162.3 3 1.414 2.00   40 100 10,000 4 1.58 2.51   50 316.23 105 5 1.78 3.162   60 1000 106 6 1.99 3.98   70 3162.3 107 7 2.24 5.01   80 104 108 8 2.51 6.31   90 31,623 109 9 2.82 7.94   100 105 1010 10 3.162 10   110 316.233 1011 12 3.98 15.8   120 106 1012 15 5.62 31.62   130 316.234 1013 20 10 100   140 107 1014 The deciBel is one of the commonly misundertood aspects of sound & electrical measurement. Not a unit of measurement as such, but a convenient means of specifying the relationship between 2 values. The Bel, named after Alexander Graham Bell, is the common logarithm of a power or sound intensity ratio. Fractional exponents are commonly encountered. To avoid this, the deciBel (dB), 1 tenth of a Bel, is used. This table covers the most useful range for music & audio purposes. Given a specified impedance, Voltage or current varies as the square root of power. The Voltage ratio columns also apply to current in this case. So 20dB (2 Bels) is a power ratio of 10 to the power of 2 (100). The Voltage & current ratio is the square root, or just 10 (101). For values not in the table the deciBels can be added & the ratios multiplied. For example, to find a power ratio of 5,000 to 1: 1,000 is 30dB & 5 is roughly 7dB. So the answer is 37dB, within the limitations of this table. Conversely 28dB is 8dB + 20 dB, the Voltage ratio is therefore 2.51 X 10 or 25.1 to 1. For greater accuracy with small ratios another table will be included at the end of this section. Feel free to download these tables if they are of use. We hope at some point to include the complete set of Henry Briggs logarithm tables. The dB becomes a unit with a constant as one variable. See VU, dBm & dBA etc. The table clearly shows, with multiples of 10dB, that taking off the last zero gives the exponent for power ratios. The origin of the system lies in the realm of telephony. Here matching impedances for maximum power transfer is all important. This is why it relates directly to power rather than Voltage or current. Originally called the Transmission Unit (T.U.), the name was changed in the 1920s. Early valve (vacuum tube) equipment has similiar requirements so the deciBel was adopted quickly throughout the sound engineering field in Britain & America. Continental Europe had a similiar system called the Neper, from the original spelling of John Napier's (1550 to 1617) surname. He gave the world logarithms in 1614 & his version, to base e, is the basis of the Neper. It is thus a little smaller than the Bel. It is interesting to note that common logarithms, to base 10 with log 1 = 0, arose out of discussions with Henry Briggs, in 1615 & 1616. Mr. Briggs published his first common log tables in 1617, giving credit to John Napier. Within a few years a complete set were published, for all natural numbers (positive integers) from 1 to 100,000. Thes tables are to 14 places of decimals, better than most calculators can manage today. John Napier was also the man who gave us decimal notation. Decimals were later adopted in America, for their currency after independence & by France after their revolution. Despite the system's advantages it only took over here in the second half of the 20th Century. The advent of cheap calculators finally ousted fractions from the academic mainstream. Some early 'mathematical' calculators had fractional input ability. Audio measurement using deciBels When the second term of the ratio is replaced by a constant, the deciBel becomes a unit of measurement. A number of such systems are in common use. dBm, a measurement system relative to 1 milliWatt into 600Ω, the m stands for 'milliWatt'. The Voltage corresponding to this is 0.7746 Volts RMS. Stage instruments & instruments usually work at -10dBm. Studios & broadcasting use +4dBm as a normal level. dBu, a similiar standard where 0dBu is 0.7746 Volts into any impedance, the u stands for 'unterminated'. Useful with more modern transistor equipment where impedance is less important. dBv, an earlier name for dBu, the small v stands for Volts. No longer used as many writers etc. confused it with dBV (capital V). dBV, similiar to dBu, but the standard reference is one Volt, the capital V stands for Volt. Our Bruel & Kjaer test equipment uses this standard. VU, Volume Unit, a system for use with averaging sound level meters. Calibration is similiar to dBm, but the correlation only holds for steady sine waves. Normally set so that 0VU is +4dBm. These meters are of little use with digital recording. dBW, a power measurement system where the reference standard is 1 Watt. Used for higher power systems & is less common. dBK, in this standard 0dBK is one KiloWatt (1000 Watts). It is hard to see where this fits into most music use. dBFS, a standard for digital recording, FS stands for Full Scale. 0dBFS is the level at which all bits of the digital code are set to 1, The signal can not get any greater than this, digital systems have zero headroom. For reproduction without clipping, the peak signal must be less than or equal to 0dBFS. Thus all working levels are negative figures. Acoustic measurement dBi, my proposed name for the unit of sound intensity, the i stands for intensity. The dB name is often quoted for 'unweighted' measurement. As this is the established name for a dimensionless ratio, it is confusion by & for the uneducated. A 20dB increase can change from loud to deafening, a 20dB level is very quiet. Where is the sense in that? 0dBi (or 0dB), the reference level, is 1 picoWatt (1 Watt x 10-12) per square metre. This miniscule figure is the measured threshold of hearing for a healthy young human @ 1 Kc/s. This is the acoustic equivalent of electrical power. The level at which hearing damage can occur is 120dBi, one acoustic Watt. This is 1012, 1 Imperial billion (American trillion) times greater. So the range of human hearing is quite wide, I don't know how many people volunteered to go deaf to get this figure. One of the reasons for using a logarithmic scale is this wide range of hearing perception. dBA, a similiar measure, but with the reference set to a curve approximating the human ear's frequency response. two other curves, dBB & dBC are rarely used. dBSPL, sound pressure level. 0dBSPL is set at 20 microPascals (2 X 10-5 Newtons per square metre), the threshold of hearing. This measure is the equivalent of electrical Volts. 120dBSPL is again the level of potential hearing damage. Acoustic displacement, or air movement is the equivalent of electrical current. Difficult to measure directly at the frequencies & amplitudes involved. It is approximately calculated from dBSPL readings at two close points, allowing for the specific mass & density of air. A means of directly measuring minute air displacements at audio frequencies has now been devised. The technique is potentially highly accurate, allthough difficult to calibrate, since no precise standard exists. We may have the nearest thing to a perfect microphone, with essentially similiar mass to air. Wrong Usage & Confusion. There is an active campaign to get rid of the good old deciBel that has served us well. It would be replaced by measurements from the SI system of units. The reason is the ignorance & confusion that has plagued the dB for many years. It will be a shame if such a useful system for engineers becomes obsolete. Just because those who don't know what they are talking about, insist on talking about it. The 'dumbing down' of much of the world's population has found its way into the technical, or pseudo technical writing 'profession'. As an example take the specification of a typical stage performance loudspeaker driver. The 'sensitivity' figure is of interest, for an efficient model this may be 100dB, by this the writer usually means 100dBA. In some cases the reference power is included, less often the measurement distance, the frequency is seldom mentioned. If the typical power of 1 Watt is included, it can be inferred that at 100 Watts the threshold of hearing damage (120dBA), will be reached. Exceeded by 3dB at 200 Watts. This is a common misconception, the sensitivity specification is an 'output', not a listener's auditory 'input'. If the distance is given, it is typically 1 Metre for a driver of this power. No-one will be listening to a 100 or 200 Watt amplifier flat out at 1 metre. In an open space, sound follows the inverse square law, at 2 metres the intensity is one quarter, 6dB dowm. At 10 metres it is one hundredth, 20dB down. In a room full of people &/or soft furnishings sound will be further attenuated. It is reinforced by significant reverberation. Formulae © Ron Lebar, Author. Updated: 14-5-2005. Loaded:

We Wish ALL the World Peace, Justice, Equality, Prosperity & an End to Fanaticism.