Sine waves, audio frequencies & tone generation.
For electrical engineering, electronics & music technology.
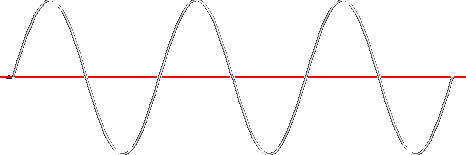
Three cycles of a sine wave, 6π radians or 1080 degrees. A graphical representation.
A historic perspective.
A Sine wave is the stuff of which sound and music is made. Also just about everything else in the universe. This sweeping assertion may need some explaining, but first a little history.

The study of circles & angles was developed by the ancient Greeks. The origins are much older. Earlier civilisations across the globe had built up a vast store of knowledge. Much of this we are only now beginning to rediscover.
Early Greek trigonometry uses chords as the basis of many calculations, in the arithmetical sense, not the musical kind. At one time 24 steps were used to measure a circle, the number of hours in a day. Hipparchus, the father of trigonometry, introduced the Babylonian 360 degree circle to the Greeks. This was based on the number of days once thought to make up a year.
Each degree was divided into 60 minutes, which were further divided into sixty seconds. This system is the one we use today, unchanged.
He accurately measured the solar year, sidearal year & hence the earth's precession. Also measuring the distance to the moon correctly, amazing feats for the second century B.C. Several centuries into A.D. most people in this country still thought the earth was flat.
Centuries later Claudius Ptolemy expanded on Hipparchus' ideas and findings. It is his writings that give most of the available information about the earlier master.
The Romans, under Julius Ceasar, standardised the year to 365 & a quarter days (almost), as it still is. They also renamed the seventh month after their emperor. The concept of degrees was not altered. Just as well, otherwise we would now be battling with 365.24219 degrees to a circle.
A more 'scientific' measure of angles is often used today. The Radian, a circle divided by 2 X pi ( π ), has advantanges in certain calculations, particularly complex ones. Being coarser & far less intuitive it has never gained general acceptance or entered common usage.
A military measure is Gradients, 400 units, called Grads, to a circle. The point of this alternative scale escapes me. Meant to be metric, but not used in metric countries. Maybe military officials thought 360 was too complex a number for soldiers & rounded it up. Rather akin to Europe's pointless rounding up of our Horsepower, from 746 tp 750 Watts.
A later sophistication in trigonometry, pioneered in India, was the use of sines. A subtle & elegant solution to the tricky mathematics of chords. Simply put, a sine is a half chord. More accurately, it is half the chord of twice the angle.
As a result of this small change, the discipline became more powerful & capable of considerable further development. India also gave us the concept of zero, making possible much of the sophisticated mathematics we take for granted today.
Sine is a corruption of the Latin word 'sinus', a fold or curve. This seems to be an incorrect translation of the Arabic 'jayb', a fold in a garment. The correct word is probably 'jiba, a phonetic version of the Sanskrit word 'jiva', a bowstring. Jiba, usually abbreviated to 'jb', was otherwise meaningless in medieval Arabic. This probably explains the mistake.
Indian mathematics made its way into Arabia, after the invasion of India by Muslims in the early 8th century A.D. With it came their decimal numbering symbols, the place value system we use today & the concept of zero. The entire thing was introduced to Europe at the start of the 13th century by Leonardo Fibonacci, an ironic result of our invasion of Arabia, during the crusades.
From then on we were able to use numbers for more than counting pigs going to market.
This probably marks the point when the West started to become more than just a brutal military force, with some pretensions to culture. We began to develop the sciences, despite vicious & brutal opposition from the all powerful church. We may now be considered to have taken up the baton from those previous great centres of learning.

Sines & chords are closely related.
The sine of either acute angle in a right angle triangle is the length of the opposite side divided by the hypotenuse.
A chord is a line drawn between the points on a circle's circumference where two radii meet it. Assume the angle between these radii is greater than zero & less than 180 degrees. Another radius can be drawn exactly dividing that angle in two.
This creates two right angle triangles, with half the chord forming one side of each. The length of one half chord, divided by the radius is the sine of the opposite angle. Hence the statement in the history section that a sine is half the chord of twice the angle.
It can be drawn showing only the arc touched by the chord, together with the angles. The drawing then looks rather like a bow & arrow. This is the origin of the Sanskrit 'jiva', a bowstring, from which 'sine' is derived.
A unit circle, a & a2 are sines of the angles at A . Also cosines of B & B2. Likewise b is the sine of B & B2. It is also the cosine of the angles at A
If the circle is drawn in full, with 2 radii at an angle of zero, the sine is obviously zero. If one radius is then rotated steadily & the resultant sine is plotted on a graph against the changing angle a curve will be drawn. After one rotation a single cycle of a sine wave is shown. The image below shows the result, using a 'unit circle' the peak height of the waveform is one unit.
 One cycle of a sine wave, 2π radians or 360 degrees. Plotted against angular displacement.
One cycle of a sine wave, 2π radians or 360 degrees. Plotted against angular displacement.
Moving the mouse cursor to the image will plot the wave. Horizontal scale factor is c/π.
This simple movement is the basis of all harmonic motion, including that of atoms. Take the swinging pendulum of a clock & attach a laser pen. Move a sheet of photo-sensitive paper at constant speed axially underneath, the pen will draw a sine wave.
Plotting the angular displacement against time for a clock or watch balance wheel produces this curve. The vibrating tips of a struck tuning fork describe the same motion. Picking the sound up via a microphone allows it to be displayed on an oscilloscope.
Atoms of all matter radiate high frequency electromagnetic sine waves, from the rotation of their electrons. This is detected as thermal radiation (heat). When atoms get excited enough, their sine wave radiation enters the visible range of frequencies. The material glows, this radiation is usually not coherent, it covers a wide range of frequencies (heat as well as light).
In sound, particularly music, only relatively low frequencies are of interest. In particular, those between 20 cycles per second & 20,000 cycles per second. Most musical instruments produce fundamental pitches over a narrower range than this.

Frequency is the repetition rate of all cyclic phenomena, it is measured in cycles per second (c/s). The European term for this value, Hertz (Hz) is now commonly used. Named after German Physicist, Heinrich Hertz, the first to publish data on experiments with wireless transmission. Sine waves are cyclic, rotating in phase through 360 degrees continuously, hence cycles per second.
Waveforms of many cyclic phenomena, including most sounds, appear at first glance not to resemble sine waves. Analysis shows that these consist of a number of sine waves, of different frequencies, occurring at the same time. The basic frequency of such waveforms is considered to be that of the slowest significant component. This is called the fundamental frequency or pitch.
Waveform components whose frequency is an integral multiple of the fundamental are called harmonics. Usually these are of lesser amplitude. Integral fractions are sub-harmonics. These may have harmonics of their own, as in the Hammond's Sub-Octave & Sub-Third.
In music, waveforms are usually complicated, due to the presence of other notes, played at the same time. Such combinations are called chords if the results are harmonious, i.e. pleasant to listen to. Other combinations are called dischords, or described as 'atonal'. Tastes vary as to which category a particular combination fits.
Chords in music should not be confused with the geometric kind.
In many cases, although the fundamental pitches are pleasant in combination, one or more of the harmonics are not. This is a common feature of instruments with strong harmonics, such as harpsichords. Often a chord sequence that is harmonious on one instrument is atonal on another.
Even the piano, an instrument with carefully controlled harmonics, exhibits this characteristic to some extent. Particularly in the higher registers, in part due to inaccuracies in the harmonic relationship. My term for this is 'harmonic deviation', in America it is called 'inharmonicity'. It, together with harmony, are complex subjects, worthy of their own page, see 'Harmony & Tuning'.


Sines. © Ron Lebar, Author. Updated: 15-5-2005. Loaded:
|
| We Wish ALL the World Peace, Justice, Equality, Prosperity & an End to Fanaticism. |